Como encontrar variância usando Python

este artigo foi publicado originalmente em Construídas em por Eric Kleppen.

A variação é uma estatística poderosa usada em análise de dados e aprendizado de máquina. É uma das quatro principais medidas de variabilidade, juntamente com o intervalo, intervalo interquartil (IQR) e desvio padrão. Compreender a variação é importante porque fornece informações sobre a disseminação de seus dados e pode ser usado para comparar diferenças em grupos de amostra ou identificar recursos de modelagem importantes. A variação também é usada no aprendizado de máquina para entender as mudanças no desempenho do modelo devido ao uso de diferentes amostras de dados de treinamento.

Calcular a variação é fácil usando Python. Antes de mergulhar no código Python, primeiro explicarei o que é variância e como você pode calculá-la. Ao ultimate deste instructional, você terá uma melhor compreensão de por que a variância é uma estatística importante, juntamente com vários métodos para calculá-la usando Python.

O que é variância?

A variância é uma estatística que mede a dispersão. A baixa variância indica que os valores são geralmente semelhantes e não variam muito da média, enquanto a alta variância indica que os valores estão mais dispersos da média. Você pode usar a variação em um conjunto de amostra ou em toda a população, pois o cálculo inclui todos os pontos de dados no conjunto fornecido. Embora o cálculo seja um pouco diferente quando você está analisando uma amostra as opposed to população, você pode calcular a variância como a média das diferenças quadradas da média.

Como a variância é um valor ao quadrado, pode ser difícil interpretá-la em comparação com outras medidas de variabilidade, como o desvio padrão. Independentemente disso, revisar a variação pode ser útil; fazer isso pode tornar mais fácil para você decidir qual testes estatísticos para usar com seus dados. Dependendo dos testes estatísticos, a variação desigual entre as amostras pode torcer ou tendência resultados.

Um dos populares testes estatísticos que aplica a variância é chamado de teste de análise de variância (ANOVA). Um teste ANOVA é usado para avaliar se alguma das médias do grupo é significativamente diferente uma da outra ao analisar uma variável independente categórica e uma variável dependente quantitativa. Por exemplo, digamos que você queira analisar se o uso da mídia social afeta as horas de sono. Você pode dividir o uso de mídia social em diferentes categorias, como baixo uso, uso médio e alto uso e, em seguida, executar um teste ANOVA para avaliar se há diferenças estatísticas entre as médias do grupo. O teste pode mostrar se os resultados são explicados por diferenças de grupo ou diferenças individuais.

Como você encontra a variação?

O cálculo da variância para um conjunto de dados pode diferir com base no fato de o conjunto ser a população inteira ou uma amostra da população.

A fórmula para calcular a variância de uma população inteira é assim:

σ² = ∑ (Xᵢ— μ)² / N

Explicação da fórmula:

• σ² = variância populacional
• Σ = soma de…
• Χᵢ = cada valor
• µ = média populacional
• Ν = número de valores na população
• Usando um exemplo de intervalo de números, vamos percorrer o cálculo passo a passo.

Exemplo de intervalo de números: 8, 6, 12, 3, 13, 9

Encontre a média populacional (μ):

Calcule os desvios da média subtraindo a média de cada valor.

Eleve ao quadrado cada desvio para obter um número positivo.

Soma os valores ao quadrado.

Divida a soma dos quadrados por N ou n-1.

Como estamos trabalhando com toda a população, dividiremos por N. Se estivéssemos trabalhando com uma amostra da população, dividiríamos por n-1.

69,5/6 = 11,583

Aí temos! A variância da nossa população é de 11.583.

Por que usar n-1 ao calcular a variância da amostra?

A aplicação de n-1 à fórmula é chamada Correção de Bessel, em homenagem a Friedrich Bessel. Ao usar amostras, precisamos calcular a variância estimada para a população. Se usássemos N em vez de n-1 para a amostra, a estimativa seria tendenciosa, potencialmente subestimando a variância populacional. O uso de n-1 tornará a estimativa de variância maior, superestimando a variabilidade nas amostras, reduzindo assim os vieses.

Vamos recalcular a variância fingindo que os valores são de uma amostra:

Como podemos ver, a variância é maior!

Calculando a variação usando Python

Agora que fizemos o cálculo à mão, podemos ver que completá-lo para um grande conjunto de valores seria muito tedioso. Felizmente, o Python pode lidar facilmente com o cálculo para dados muito grandes. Vamos explorar dois métodos usando Python:

• Escreva nossa própria função de cálculo de variância
• Use a função integrada do Pandas

Escrevendo uma função de variação

À medida que começamos a escrever uma função para calcular a variância, pense nos passos que demos ao calcular manualmente. Queremos que a função receba dois parâmetros:

• população: uma matriz de números
• is_sample: um booleano para alterar o cálculo dependendo se estamos trabalhando com uma amostra ou população

Comece definindo a função que recebe os dois parâmetros.

Em seguida, adicione lógica para calcular a média populacional.

Depois de calcular a média, encontre as diferenças da média para cada valor. Você pode fazer isso em uma linha usando uma compreensão de lista.

Em seguida, eleve ao quadrado as diferenças e some-as.

Por fim, calcule a variância. Usando uma instrução If/Else, podemos utilizar o parâmetro is_sample. Se is_sample for true, calcule a variância usando (n-1). Se for falso (o padrão), use N:

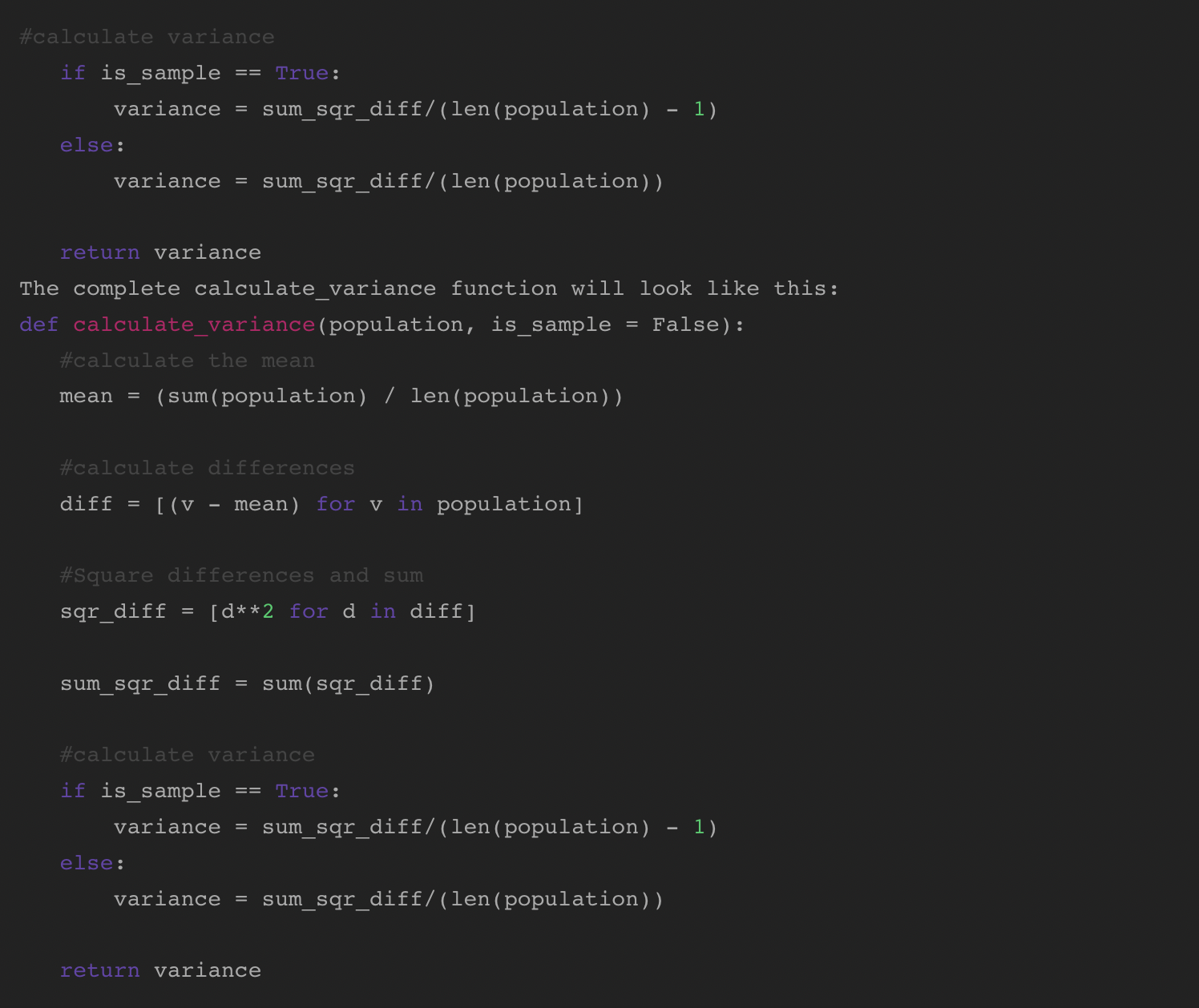
Podemos testar o cálculo usando o intervalo de números que processamos manualmente:

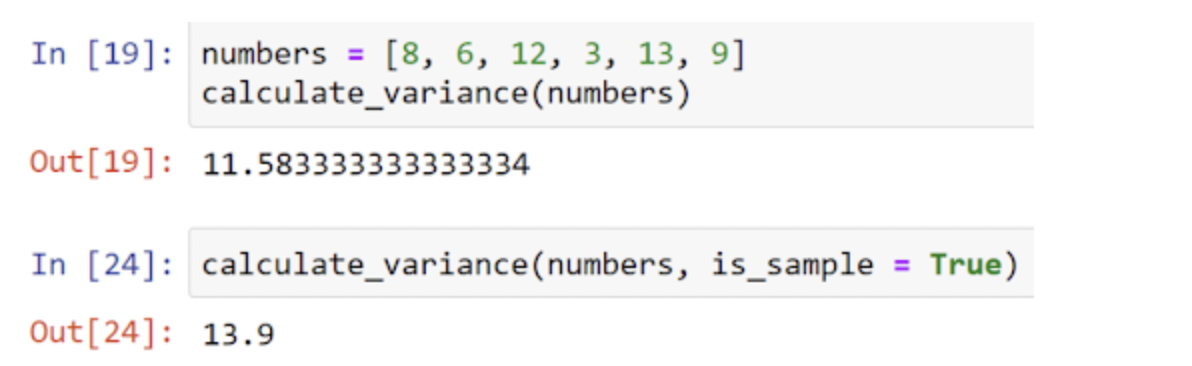
Encontrando variação usando Pandas

Embora possamos escrever uma função para calcular a variação em menos de 10 linhas de código, existe uma maneira ainda mais fácil de encontrar a variação. Você pode fazer isso em uma linha de código usando Pandas. Vamos carregar alguns dados e trabalhar com um exemplo actual de encontrar variância.

Carregando dados de exemplo

O exemplo do Pandas u.s.a. o Desafio de preços BMW conjunto de dados do Kaggle, que pode ser baixado gratuitamente. Comece importando a biblioteca do Pandas e, em seguida, lendo o arquivo CSV em um quadro de dados do Pandas:

Podemos contar o número de linhas no conjunto de dados e exibir as cinco primeiras linhas para garantir que tudo seja carregado corretamente:

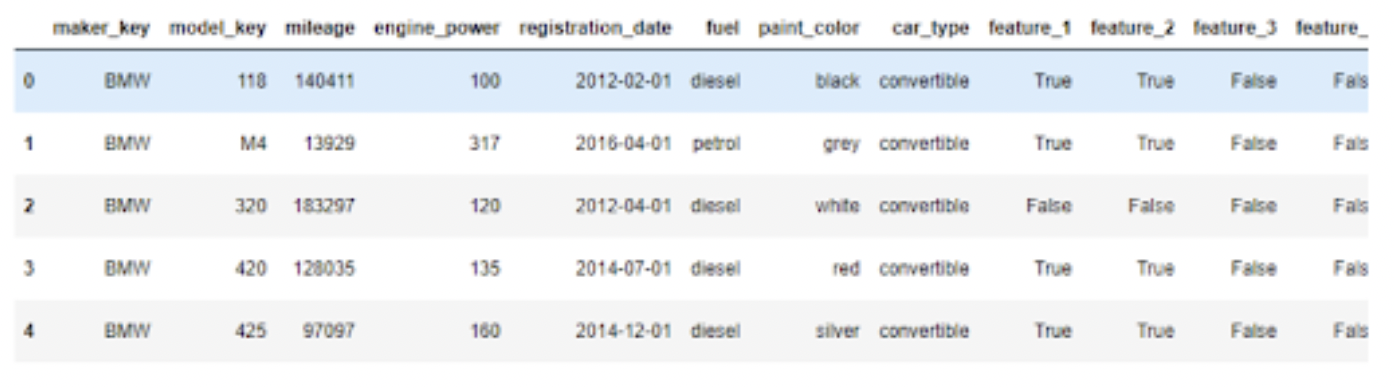
Encontrando a variação para os dados da BMW

Como o conjunto de dados da BMW é de 4.843 linhas, calcular isso manualmente não seria divertido. Em vez disso, podemos simplesmente inserir a coluna do quadro de dados em nossa função calculate_variance e retornar a variância. Vamos encontrar a variação para as colunas numéricas milhagem, motor_potência e preço.

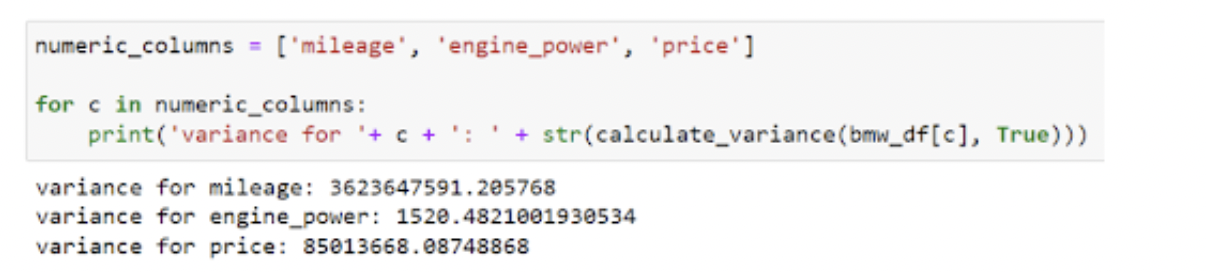
Usando a função Pandas var()

Caso esqueçamos o cálculo da variância e não possamos escrever nossa própria função, o Pandas possui uma função interna para calcular a variância chamada var(). Por padrão, ele think uma população amostral e u.s.a. n-1 no cálculo; no entanto, você pode ajustar o cálculo passando o argumento ddof=0.

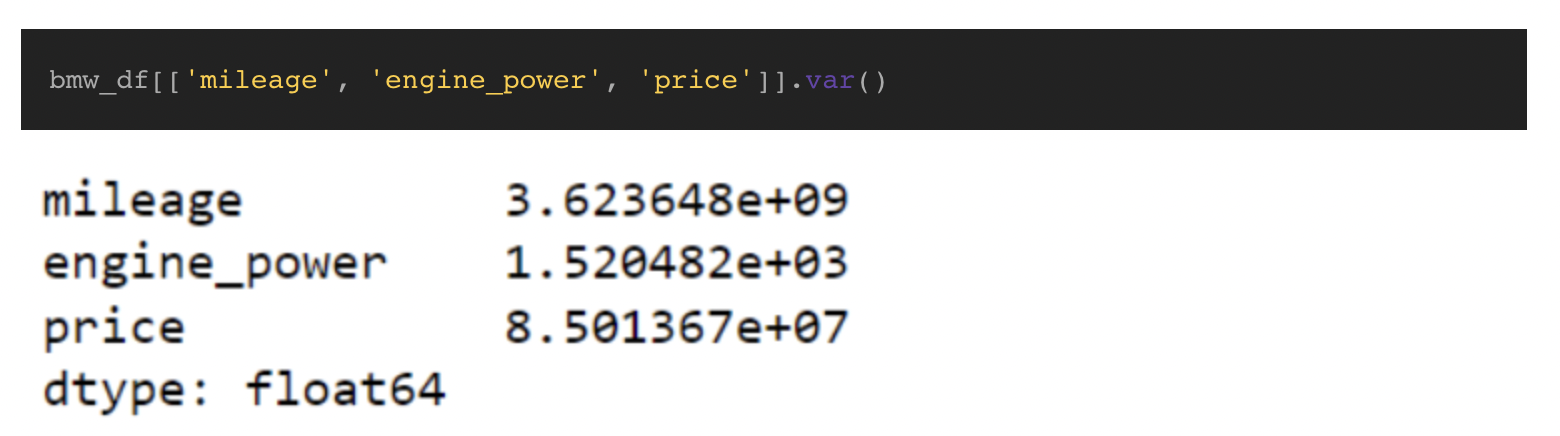
Como podemos ver, a função Var() corresponde aos valores produzidos pela nossa função calculate_variance, e é apenas uma linha de código. Analisando os resultados, podemos ver que a quilometragem tem uma alta variância, o que significa que os valores tendem a variar muito da média. Isso faz sentido porque muitos fatores influenciam a distância que uma pessoa precisa dirigir. Em comparação, engine_power tem uma variação baixa, o que indica que os valores não variam muito da média.

O take-away

Compreender a variação pode ser uma parte importante da análise de dados e do aprendizado de máquina porque você pode usá-lo para avaliar as diferenças do grupo. A variação também afeta quais testes estatísticos podem nos ajudar a tomar decisões baseadas em dados. Valores de médias de alta variância estão muito dispersos da média, enquanto que os números de baixa variância não estão amplamente dispersos da média. Se tivermos um pequeno conjunto de valores, é possível calcular a variância manualmente em apenas cinco etapas. Para grandes conjuntos de dados, vimos como é simples calcular a variação usando Python e Pandas. A função Var() no Pandas calcula a variação das colunas numéricas em um quadro de dados em apenas uma linha de código, o que é bastante útil!